His law is: Stokes' Theorem for E is. Combining these two equations yields for any surface S: from which physicists conclude: c E - (B / t) = 0. As the differential form of Faraday's Law. For convenience, we have chosen units for E and B such the constants c apearing in Ampere's Law and Faraday's Law are the same. The differential form of the Maxwell-Faraday Equation (Equation 8.8.6) relates the change in the electric field with position to the change in the magnetic field with time. Now that is arguably new and useful information. Starting with the differential form of Faraday’s law ∇ × E = − ∂ B ∂ t It is a local statement. We first integrate on both sides about an arbitrary surface Σ.
Homework Statement:
(a) Find the induced current density as a function of distance from the axis of the disk.
(b) What is the direction of this current?
Relevant Equations:
Faraday's Law In Differential Formation

Faraday's Law Equation

EMF: ##varepsilon = - frac {d phi} {dt}##
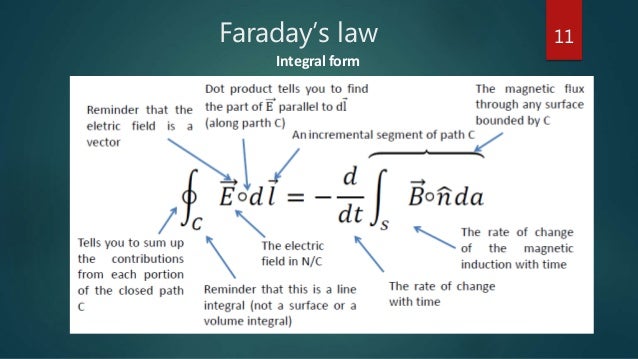
Faraday's Law: ##oint vec E cdot d vec l = - frac {d phi} {dt}##
Current density and E-field relationship: ##vec J = sigma vec E##
Define Faraday's Law
Hello I'm having trouble finding the right way to apply Faraday's law to this question. I've found the flux through the disc:
##phi = vec A cdot vec B = B_{0} sin{omega t} left( frac D 2 right)^2 pi ##
and the EMF:
##varepsilon = - frac {d phi} {dt} = -B_{0} omega cos{omega t} left( frac D 2 right)^2 pi##
Now to find the current density ##vec J## I believe I need to find the electric field ##vec E## using Faraday's law. I've seen it applied to a circular wire in a magnetic field in where the closed loop is the wire itself. I'm not sure how to apply this to a disk of thickness h though. Do I need to add up the contributions of circular strips with radii between 0 and ##frac D 2## and thickness da?
I'm also not sure about how to make it a 'function of distance from the axis of the disk'.
##phi = vec A cdot vec B = B_{0} sin{omega t} left( frac D 2 right)^2 pi ##
and the EMF:
##varepsilon = - frac {d phi} {dt} = -B_{0} omega cos{omega t} left( frac D 2 right)^2 pi##
Now to find the current density ##vec J## I believe I need to find the electric field ##vec E## using Faraday's law. I've seen it applied to a circular wire in a magnetic field in where the closed loop is the wire itself. I'm not sure how to apply this to a disk of thickness h though. Do I need to add up the contributions of circular strips with radii between 0 and ##frac D 2## and thickness da?
I'm also not sure about how to make it a 'function of distance from the axis of the disk'.

